How To Draw Visual Confusion Matrix

GETTING STARTED

Visual Guide to the Confusion Matrix

Binary and Multi-class Defoliation Matrices Explained

We've congenital a machine learning model to classify whether or non a patient has some kind of virus. A patient can be in two states: they either accept the virus or they don't.

We represent a patient as a circle. Filled-in means they have the virus. Unfilled means they don't. — We represent a patient equally a circle. Filled-in means they take the virus. Unfilled means they don't. (Image past author)

For any given patient our model produces a score betwixt 0 and 1. A score of 1 ways the model is predicting that the patient does have the virus, and 0 a prediction that they don't.

Predicted scores are represented as a square. The more filled-in, the higher the score. (Image by author)

If we take a selection of 100 patients, where a portion of those patients take the virus, then we have the model produce a score for each patient, how can nosotros evaluate the performance of the model?

A grid of 100 circles representing the actual values. Filled-in circles are positive for the virus, and non-filled circles are negative. On the right is the predicted scores with a grid of 100 squares. Each square is filled in relative to its score; a score of 0.5 has a cell filled-in halfway — (Image by writer)

At that place are many different means nosotros can evaluate how well the model'southward scores friction match the bodily values. For this example we'll exist taking a look at the confusion matrix where we utilise a grid to visually evaluate the results.

Threshold

To make up one's mind if the scores refer to a positive or negative prediction of the virus, we'll need to decide where to threshold them. We can practise this by choosing a value in which all scores greater than this value are considered positive predictions and all below are negative.

Where we place this threshold value determines how biased our model is to the 2 classes. A low threshold results in a bias towards a positive output and the reverse is true for a high threshold. Choosing the correct threshold depends on what the goal of your model is and how it will be used. For at present though we'll simply selection a threshold of 0.v.

Converting a score between 0 and 1 and thresholding it so it outputs as 1 or 0 — (Epitome by author)

Comparing Actual vs Predicted

Now that we've practical the threshold to each output score, we can compare our outputs to the bodily patients.

Actual values + predicted scores = true-positive, false-negative, false-positive, true-negative — (Paradigm past author)

In that location are four distinct groups that sally when we compare the results.

Each comparison of the actual values and predicted classes are seperated into the four categories. Starting in the top-left and going clockwise: True-positive, false-negative, true-negative, false-positive — (Image by writer)

True Positive (TP): The predicted class was positive for the virus and the actual form was positive.
False Positive (FP): The model predicted positive and the actual form was negative.
Fake Negative (FN): The predicted class was negative and the bodily grade was positive.
True Negative (TN): The predicted class was negative for the virus and the actual class was also negative.

The get-go word, which is a boolean of either True or False, is True when the prediction and actual values match and False otherwise. The second word refers to the course: in this example information technology can be either positive or negative. A model performing well would take primarily truthful positives and true negatives which we'll exist able to visualize in a confusion matrix.

Defoliation Matrix

By counting each of the four categories we can display the results in a 2 by 2 grid. Along the y-axis is the actual values (The patients and their label of either positive or negative) and along the ten-centrality is our prediction. Each quadrant of this grid refers to one of the iv categories then by counting the results of a quadrant nosotros tin can place the value in that prison cell.

Binary-class Confusion matrix with the label of each quadrant. Starting in the top left and going clockwise: true-positive, false-negative, true-negative, false-positive — Each quadrant refers to ane of the four possibilities. (Image past author)

Information technology's helpful to color each quadrant with the proportion that cells value takes up relative to all of the cells in the row. Since the true positives and truthful negatives are along the diagonal from top-left to lesser-right, we can presume the model is performing well if this diagonal is highlighted.

Two binary-class confusion matrices with a model performing well on the left (The diagonal has the highest values) and a poorly performing model on the right (The model over-classifies the positive class and so the bottom left cell is filled in) — (Image by author)

Should the model perform poorly, information technology is piece of cake to identify what went wrong as i of the diagonal cells will only be slightly filled and another on that row will exist highlighted. For the faulty model above, the number of false positives are a lot higher than the number of truthful negatives, so our model is over predicting the positive course (the model is predicting that the patient has the virus when they don't).

We can get back to the model and make changes based on this information. Perchance nosotros modify how we railroad train it, or the architecture of the model itself. This may too be a good fourth dimension to modify the threshold to a college value and so the outputs are biased towards the negative class. Binary-course confusion matrices like this can aid guide our conclusion making when edifice a classification model.

Multi-grade Defoliation Matrix

After a successful career, we've retired from the world of medicine and have decided to accept up a hobby in wildlife photography. To help organize the photos we take, we've built a classifier model to label which animals are in the photos. How can we use a confusion matrix to evaluate on multi-form problems?

Classification of a lion. The lion has a green box around it identifying where in the image it is, and the predicted scores for the four classes are to the right of it. — Lion image from Unsplash past Mika Brandt

Like before we nonetheless need to make up one's mind which class the output scores accept predicted. Rather than perform thresholding, we'll pick the output with the highest probability and consider that the grade the model is predicting.

Table of predicted scores for each of the four classes where the highest score is highlighted — Highlighted cells are the highest predicted score for a photograph. (Image by writer)

The confusion matrix is prepare in a like style as before except now there'due south two extra classes. The general idea is the same also: for each prediction, we compare the upshot confronting the labeled data we're evaluating on. If our model predicts elephant and the epitome did really incorporate an elephant, that'south a right classification! We tin then add that result to its associated cell. The same goes for when our model is wrong, such as when the predicted grade is monkey just the photo actually independent a king of beasts.

Afterward comparing each predicted class with the associated label, the defoliation matrix starts to expect like to the binary-class situation. The diagonal here is where the model performed accurately and will contain high values in these cells relative to other cells in that same row.

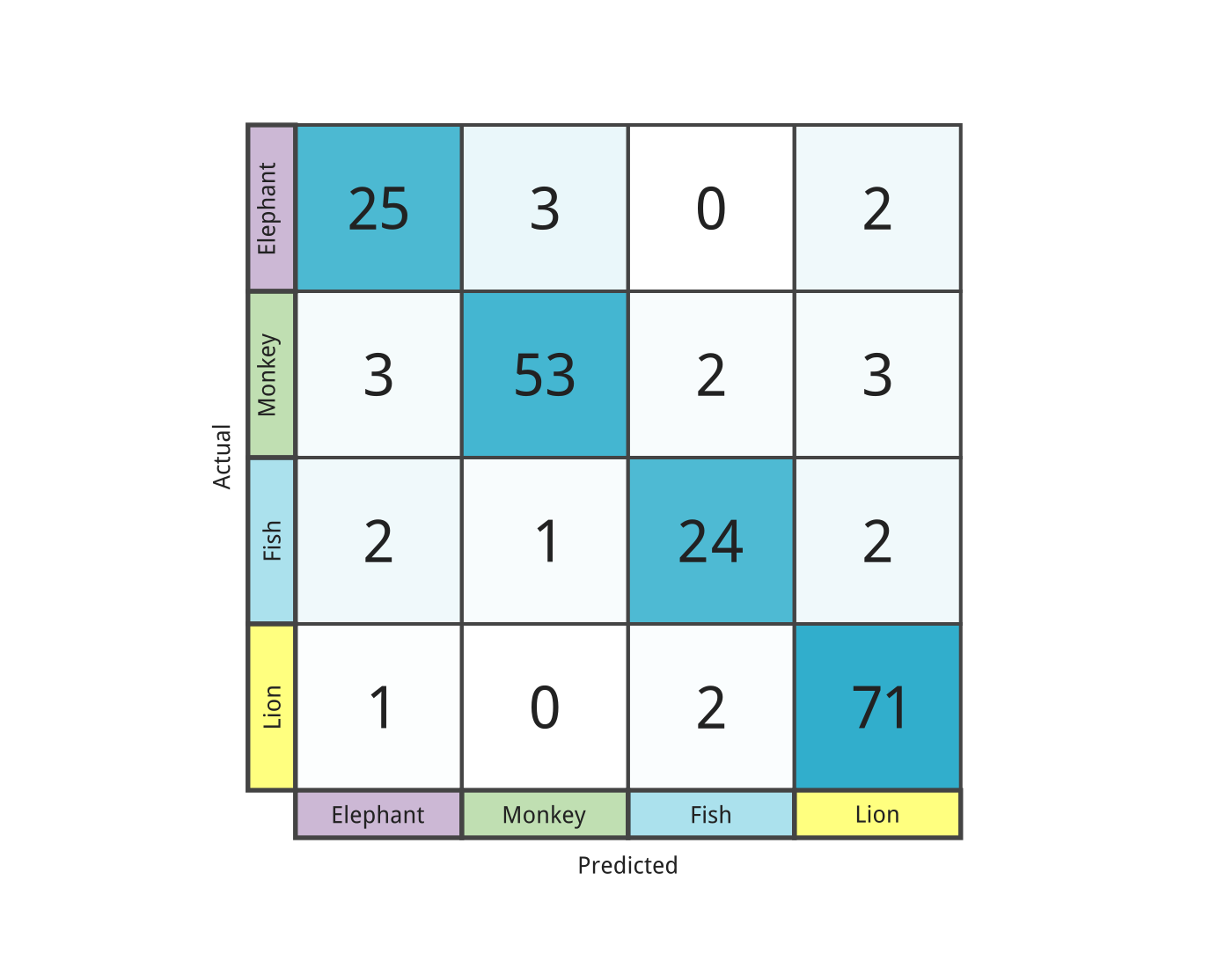
Multi-class confusion matrix where the majority of predicted scores match the actual values — (Image by author)

Additionally, nosotros can still identify where all truthful-positive, fake-positive, truthful-negative and fake-negatives are relative to any form. Let'due south say we're interested in how our model is performing on the class fish:

Animated gif of the true-positive, false-positive, true-negative and false-negative sections of a multi-class confusion matrix relevant to a single class — (Image by author)

True Positive (TP): A classification of fish when the actual class is a fish.
False Positive (FP): A nomenclature of fish but information technology was actually one of the other 3 classes.
False Negative (FN): A nomenclature of something other than fish, merely the actual class was a fish.
Truthful Negative (TN): A nomenclature of something other than fish, and the actual class was something other than fish. (The prediction and actual classes do not have to match as we only care almost the fish course).

When the classification is incorrect we can visually see exactly where the model was incorrect. Hither nosotros can see that our model is classifying lions every bit monkeys:

Multi-class confusion matrix where the prediction for lion is often a monkey. In this case, the model is on the class lion — (Image by author)

Hopefully this model isn't deployed in any high-risk environments!

Want to back up more content like this? Sign up for Medium'south membership using this link https://mlee-articles.medium.com/membership and a portion of your membership will go to the development of futurity content